Functions¶
Solution of least squares by the normal equations
1 2 3 4 5 6 7 8 9 10 11 12 13def lsnormal(A, b): """ lsnormal(A, b) Solve a linear least squares problem by the normal equations. Returns the minimizer of ||b-Ax||. """ N = A.T @ A z = A.T @ b R = scipy.linalg.cholesky(N) w = forwardsub(R.T, z) # solve R'z=c x = backsub(R, w) # solve Rx=z return x
About the code
cholesky is imported from scipy.linalg.
Solution of least squares by QR factorization
1 2 3 4 5 6 7 8 9 10 11def lsqrfact(A, b): """ lsqrfact(A, b) Solve a linear least squares problem by QR factorization. Returns the minimizer of ||b-Ax||. """ Q, R = np.linalg.qr(A) c = Q.T @ b x = backsub(R, c) return x
QR factorization by Householder reflections
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21def qrfact(A): """ qrfact(A) QR factorization by Householder reflections. Returns Q and R. """ m, n = A.shape Qt = np.eye(m) R = np.copy(A) for k in range(n): z = R[k:, k] w = np.hstack((-np.sign(z[0]) * np.linalg.norm(z) - z[0], -z[1:])) nrmw = np.linalg.norm(w) if nrmw < np.finfo(float).eps: continue # skip this iteration v = w / nrmw # Apply the reflection to each relevant column of R and Q for j in range(k, n): R[k:, j] -= 2 * np.dot(v, R[k:, j]) * v for j in range(m): Qt[k:, j] -= 2 * np.dot(v, Qt[k:, j]) * v return Qt.T, np.triu(R)
Examples¶
3.1 Fitting functions to data¶
Example 3.1.1
Here are 5-year averages of the worldwide temperature anomaly as compared to the 1951–1980 average (source: NASA).
year = arange(1955,2005,5)
y = array([ -0.0480, -0.0180, -0.0360, -0.0120, -0.0040,
0.1180, 0.2100, 0.3320, 0.3340, 0.4560 ])
fig, ax = subplots()
ax.scatter(year, y, color="k", label="data")
xlabel("year")
ylabel("anomaly (degrees C)")
title("World temperature anomaly");
A polynomial interpolant can be used to fit the data. Here we build one using a Vandermonde matrix. First, though, we express time as decades since 1950, as it improves the condition number of the matrix.
from scipy import linalg
t = (year - 1950) / 10
V = vander(t)
c = linalg.solve(V, y)
print(c)[ 1.03111111e-02 -2.54666667e-01 2.69480635e+00 -1.59628889e+01
5.80155778e+01 -1.33273472e+02 1.91960567e+02 -1.65455972e+02
7.63617381e+01 -1.41140000e+01]
The coefficients in vector c are used to create a polynomial. Then we create a function that evaluates the polynomial after changing the time variable as we did for the Vandermonde matrix.
p = poly1d(c) # convert to a polynomial
tt = linspace(1955, 2000, 500)
ax.plot(tt, p((tt - 1950) / 10), label="interpolant")
ax.legend();
fig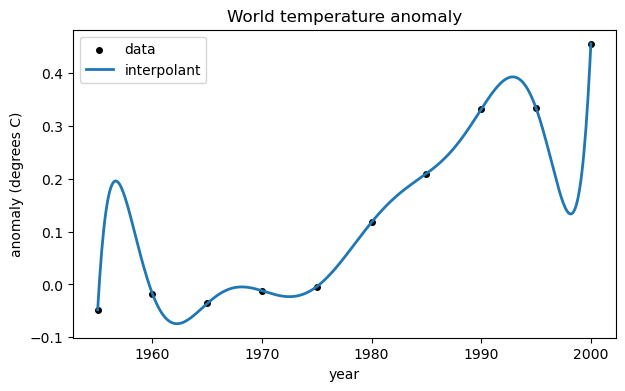
As you can see, the interpolant does represent the data, in a sense. However it’s a crazy-looking curve for the application. Trying too hard to reproduce all the data exactly is known as overfitting.
Example 3.1.2
Here are the 5-year temperature averages again.
year = arange(1955, 2005, 5)
y = array([-0.0480, -0.0180, -0.0360, -0.0120, -0.0040,
0.1180, 0.2100, 0.3320, 0.3340, 0.4560])
t = (year - 1950) / 10The standard best-fit line results from using a linear polynomial that meets the least-squares criterion.
Tip
Backslash solves overdetermined linear systems in a least-squares sense.
V = array([ [t[i], 1] for i in range(t.size) ]) # Vandermonde-ish matrix
print(V.shape)(10, 2)
from scipy.linalg import lstsq
c, res, rank, sv = lstsq(V, y)
p = poly1d(c)
f = lambda year: p((year - 1950) / 10)
```{code-cell}
fig, ax = subplots()
ax.scatter(year, y, color="k", label="data")
yr = linspace(1955, 2000, 500)
ax.plot(yr, f(yr), label="linear fit")
xlabel("year")
ylabel("anomaly (degrees C)")
title("World temperature anomaly");
ax.legend();If we use a global cubic polynomial, the points are fit more closely.
V = array([ [t[i]**3,t[i]**2,t[i],1] for i in range(t.size) ]) # Vandermonde-ish matrix
print(V.shape)(10, 4)
Now we solve the new least-squares problem to redefine the fitting polynomial.
Tip
The definition of f above is in terms of c. When c is changed, f is updated with it.
c, res, rank, sv = lstsq(V, y)
yr = linspace(1955, 2000, 500)
ax.plot(yr, f(yr), label="cubic fit")
fig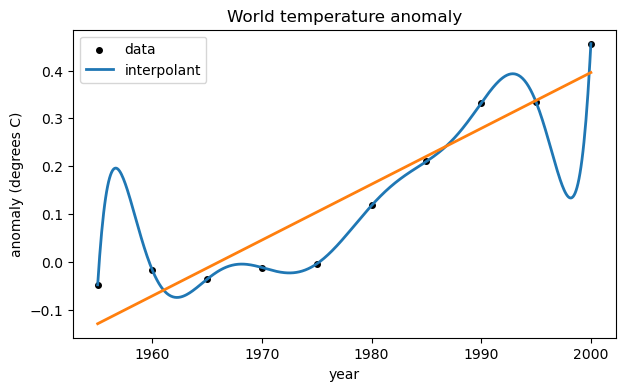
If we were to continue increasing the degree of the polynomial, the residual at the data points would get smaller, but overfitting would increase.
Example 3.1.3
a = array([1 / (k+1)**2 for k in range(100)])
s = cumsum(a) # cumulative summation
p = sqrt(6*s)
plot(range(100), p, "o")
xlabel("$k$")
ylabel("$p_k$")
title("Sequence convergence");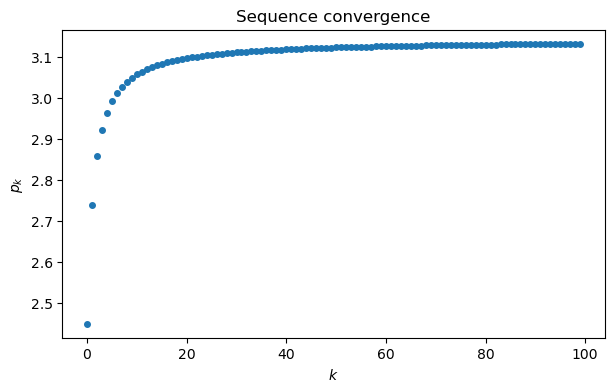
This graph suggests that maybe , but it’s far from clear how close the sequence gets. It’s more informative to plot the sequence of errors, . By plotting the error sequence on a log-log scale, we can see a nearly linear relationship.
ep = abs(pi - p) # error sequence
loglog(range(100), ep, "o")
xlabel("$k$")
ylabel("error")
title("Sequence convergence");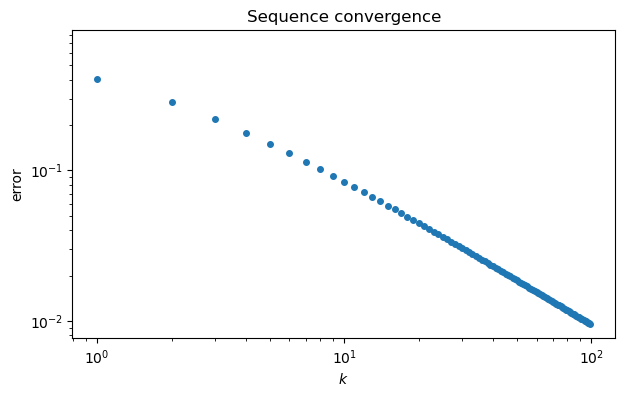
The straight line on the log-log scale suggests a power-law relationship where , or .
V = array([ [1, log(k+1)] for k in range(100) ]) # fitting matrix
c = lstsq(V, log(ep))[0] # coefficients of linear fit
print(c)[-0.18237525 -0.96741032]
In terms of the parameters and used above, we have
a, b = exp(c[0]), c[1]
print(f"b: {b:.3f}")b: -0.967
It’s tempting to conjecture that the slope asymptotically. Here is how the numerical fit compares to the original convergence curve.
loglog(range(100), ep, "o", label="sequence")
k = arange(1,100)
plot(k, a*k**b, "--", label="power fit")
xlabel("$k$"); ylabel("error");
legend(); title("Sequence convergence");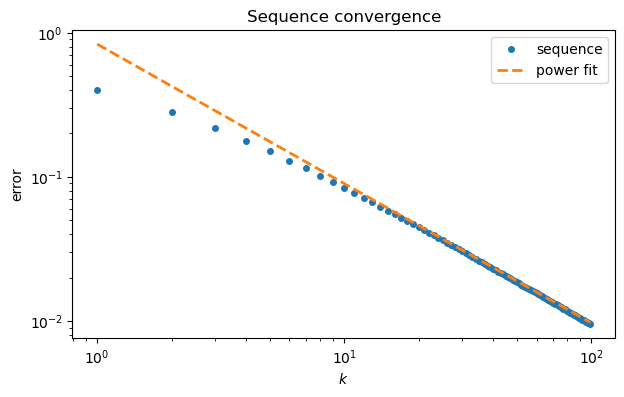
3.2 The normal equations¶
Example 3.2.1
Because the functions , , and 1 are linearly dependent, we should find that the following matrix is somewhat ill-conditioned.
from numpy.linalg import cond
t = linspace(0, 3, 400)
A = array([ [sin(t)**2, cos((1+1e-7)*t)**2, 1] for t in t ])
kappa = cond(A)
print(f"cond(A) is {kappa:.3e}")cond(A) is 1.825e+07
Now we set up an artificial linear least-squares problem with a known exact solution that actually makes the residual zero.
x = array([1, 2, 1])
b = A @ xUsing backslash to find the least-squares solution, we get a relative error that is well below times machine epsilon.
from scipy.linalg import lstsq
x_BS = lstsq(A, b)[0]
print(f"observed error: {norm(x_BS - x) / norm(x):.3e}")
print(f"conditioning bound: {kappa * finfo(float).eps:.3e}")observed error: 2.019e-10
conditioning bound: 4.053e-09
If we formulate and solve via the normal equations, we get a much larger relative error. With , we may not be left with more than about 2 accurate digits.
from scipy import linalg
N = A.T @ A
x_NE = linalg.solve(N, A.T @ b)
relative_err = norm(x_NE - x) / norm(x)
print(f"observed error: {relative_err:.3e}")
print(f"accurate digits: {-log10(relative_err):.2f}")observed error: 5.991e-02
accurate digits: 1.22
3.3 The QR factorization¶
Example 3.3.1
NumPy provides access to both the thin and full forms of the QR factorization.
A = 1.0 + floor(9 * random.rand(6,4))
A.shape(6, 4)Here is the full form:
from numpy.linalg import qr
Q, R = qr(A, "complete")
print(f"size of Q is {Q.shape}")
print("R:")
print(R)size of Q is (6, 6)
R:
[[-13.7113092 -5.61580217 -10.72107688 -8.02257453]
[ 0. -8.27422298 -6.25950658 -10.26643936]
[ 0. 0. -5.3737406 -6.4622615 ]
[ 0. 0. 0. 3.387875 ]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]
We can test that is an orthogonal matrix:
print(f"norm of (Q^T Q - I) is {norm(Q.T @ Q - eye(6)):.3e}")norm of (Q^T Q - I) is 6.171e-16
The default for qr, and the one you usually want, is the thin form.
Q_hat, R_hat = qr(A)
print(f"size of Q_hat is {Q_hat.shape}")
print("R_hat:")
print(R_hat)size of Q_hat is (6, 4)
R_hat:
[[-13.7113092 -5.61580217 -10.72107688 -8.02257453]
[ 0. -8.27422298 -6.25950658 -10.26643936]
[ 0. 0. -5.3737406 -6.4622615 ]
[ 0. 0. 0. 3.387875 ]]
Now cannot be an orthogonal matrix, because it is not square, but it is still ONC. Mathematically, is a identity matrix.
print(f"norm of (Q_hat^T Q_hat - I) is {norm(Q_hat.T @ Q_hat - eye(4)):.3e}")norm of (Q_hat^T Q_hat - I) is 3.387e-16
Example 3.3.2
We’ll repeat the experiment of Example 3.2.1, which exposed instability in the normal equations.
t = linspace(0, 3, 400)
A = array([ [sin(t)**2, cos((1+1e-7)*t)**2, 1] for t in t ])
x = array([1, 2, 1])
b = A @ xThe error in the solution by Function 3.3.2 is similar to the bound predicted by the condition number.
print(f"observed error: {norm(FNC.lsqrfact(A, b) - x) / norm(x):.3e}")
print(f"conditioning bound: {cond(A) * finfo(float).eps:.3e}")observed error: 5.186e-09
conditioning bound: 4.053e-09
3.4 Computing QR factorizations¶
Example 3.4.1
We will use Householder reflections to produce a QR factorization of a matrix.
A = 1.0 + floor(9 * random.rand(6,4))
m, n = A.shape
print(A)[[6. 4. 4. 6.]
[5. 9. 3. 4.]
[2. 1. 3. 5.]
[8. 3. 3. 5.]
[3. 7. 6. 4.]
[4. 1. 8. 4.]]
Our first step is to introduce zeros below the diagonal in column 1 by using (3.4.4) and (3.4.1).
z = A[:, 0]
v = z - norm(z) * hstack([1, zeros(m-1)])
P_1 = eye(m) - (2 / dot(v, v)) * outer(v, v) # reflectorWe check that this reflector introduces zeros as it should:
print(P_1 @ z)[ 1.24096736e+01 -4.44089210e-16 -3.33066907e-16 -4.44089210e-16
-1.11022302e-16 0.00000000e+00]
Now we replace by .
A = P_1 @ A
print(A)[[ 1.24096736e+01 9.66987557e+00 9.58929327e+00 1.07980277e+01]
[-4.44089210e-16 4.57709497e+00 -1.36004513e+00 2.57198117e-01]
[-3.33066907e-16 -7.69162014e-01 1.25598195e+00 3.50287925e+00]
[-4.44089210e-16 -4.07664806e+00 -3.97607221e+00 -9.88483012e-01]
[-1.11022302e-16 4.34625698e+00 3.38397292e+00 1.75431887e+00]
[ 0.00000000e+00 -2.53832403e+00 4.51196390e+00 1.00575849e+00]]
We are set to put zeros into column 2. We must not use row 1 in any way, lest it destroy the zeros we just introduced. So we leave it out of the next reflector.
z = A[1:, 1]
v = z - norm(z) * hstack([1, zeros(m-2)])
P_2 = eye(m-1) - (2 / dot(v, v)) * outer(v, v)We now apply this reflector to rows 2 and below only.
A[1:, 1:] = P_2 @ A[1:, 1:]
print(A)[[ 1.24096736e+01 9.66987557e+00 9.58929327e+00 1.07980277e+01]
[-4.44089210e-16 7.96828128e+00 1.54019755e+00 9.51825785e-01]
[-3.33066907e-16 3.07198988e-16 1.91379202e+00 3.66042919e+00]
[-4.44089210e-16 1.23380363e-15 -4.89602405e-01 -1.53449996e-01]
[-1.11022302e-16 -9.48115471e-16 -3.33074392e-01 8.64060986e-01]
[ 0.00000000e+00 7.56056118e-16 6.68281356e+00 1.52569162e+00]]
We need to iterate the process for the last two columns.
for j in [2, 3]:
z = A[j:, j]
v = z - norm(z) * hstack([1, zeros(m-j-1)])
P = eye(m-j) - (2 / dot(v, v)) * outer(v, v)
A[j:, j:] = P @ A[j:, j:]We have now reduced the original to an upper triangular matrix using four orthogonal Householder reflections:
R = triu(A)
print(R)[[12.40967365 9.66987557 9.58929327 10.79802772]
[ 0. 7.96828128 1.54019755 0.95182579]
[ 0. 0. 6.97662139 2.43506774]
[ 0. 0. 0. 3.25070303]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]