Basics of IVPs - Fundamentals of Numerical Computation

When $t$ is meant to be time, sometimes we write $\dot{u}$ (read “u-dot”) instead of $u'$ .

Example 6.1.1

Suppose $u(t)$ is the size of a population at time $t$ . We idealize by allowing $u$ to take any real (not just integer) value. If we assume a constant per capita birth rate (births per unit population per unit time), then

\frac{d u}{d t} = k u, \qquad u(0)=u_0

(6.1.2)

for some $k>0$ . The solution of this linear equation is $u(t)=e^{kt}u_0$ , which is exponential growth.

A more realistic model would cap the growth due to finite resources. Suppose the death rate is proportional to the size of the population, indicating competition. Then

\frac{d u}{d t} = ku - ru^2, \qquad u(0)=u_0.

(6.1.3)

This is the logistic equation. Although crude, it is still useful in population models. The solution relevant for population models has the form

u(t) = \frac{k/r}{ 1 + \left( \frac{k}{r u_0} - 1 \right) e^{-k t} }.

(6.1.4)

For $k,r,u_0>0$ , the solution smoothly varies from the initial population $u_0$ to a finite population, equal to $k/r$ , that has been limited by competition.

Linear problems can be solved in terms of integrals. Defining the integrating factor $\rho(t) = \exp\bigl[\int -h(t)\, dt \bigr]$ , the solution is derived from

\rho(t) u(t) = u_0 + \int_a^t \rho(s) g(s) \, ds.

(6.1.5)

In many cases, however, the necessary integrals cannot be done in closed form. Some nonlinear ODEs, such as separable equations, may also be solvable with a short formula, perhaps with difficult integrations. Most often, though, there is no analytic formula available for the solution.

An ODE may have higher derivatives of the unknown solution present. For example, a second-order ordinary differential equation is often given in the form $u''(t)=f\bigl(t,u,u'\bigr)$ . A second-order IVP requires two conditions at the initial time in order to specify a solution completely. As we will see in IVP systems, we are always able to reformulate higher-order IVPs in a first-order form, so we will deal with first-order problems exclusively.

6.1.1Numerical solutions¶

Example 6.1.2 (Solving an IVP)

Julia

MATLAB

Python

Example 6.1.2

The OrdinaryDiffEq package offers solvers for IVPs. Let’s use it to define and solve the initial-value problem

u'=\sin[(u+t)^2], \quad t \in [0,4], \quad u(0)=-1.

To create an initial-value problem for $u(t)$ , we must supply a function that computes $u'$ , an initial value for $u$ , and the endpoints of the interval for $t$ . The $t$ interval should be defined as (a, b), where at least one of the values is a float.

f(u, p, t) = sin((t + u)^2)     # defines du/dt, must include p argument
u₀ = -1.0                       # initial value
tspan = (0.0, 4.0)               # t interval

(0.0, 4.0)

With the data above we define an IVP problem object and then solve it. Here we tell the solver to use the Tsit5 method, which is a good first choice for most problems.

using OrdinaryDiffEq
ivp = ODEProblem(f, u₀, tspan)
sol = solve(ivp, Tsit5());

The resulting solution object can be shown using plot.

using Plots
plot(sol;
    label="solution", legend=:bottom,
    xlabel="t",  ylabel=L"u(t)",
    title=L"u'=\sin((t+u)^2)")

The solution also acts like any callable function that can be evaluated at different values of $t$ .

@show sol(1.0);

sol(1.0) = -0.7903205813665345

Under the hood, the solution object holds some information about how the values and plot are produced:

[sol.t sol.u]

15×2 Matrix{Float64}:
 0.0        -1.0
 0.0867807  -0.93483
 0.241035   -0.856617
 0.464665   -0.805668
 0.696832   -0.793614
 1.00862    -0.789925
 1.37461    -0.718601
 1.70407    -0.476837
 1.93572    -0.29033
 2.17184    -0.294994
 2.4843     -0.483948
 2.69425    -0.654121
 3.27049    -1.1783
 3.62534    -1.51729
 4.0        -1.88086

The solver initially finds approximate values of the solution (second column above) at some automatically chosen times (first column above). To compute the solution at other times, the object performs an interpolation on those values. This chapter is about how the discrete $t$ and $u$ values are computed. For now, just note how we can extract them from the solution object.

scatter!(sol.t, sol.u, label="discrete values")

Example 6.1.2

Let’s use a built-in method to define and solve the initial-value problem

u'=\sin[(u+t)^2], \quad t \in [0,4], \quad u(0)=-1.

We must create a function that computes $u'$ , an initial value for $u$ , and a vector describing the time domain.

f = @(t, u) sin((t + u)^2);
u0 = -1;
tspan = [0, 4];

These ingredients are supplied to a solver function. A standard first choice of solver is called ode45.

[t, u] = ode45(f, [0, 4], u0);
fprintf("length(t) = %d, length(u) = %d\n", length(t), length(u))

length(t) =

, length(u) =

The solution is represented as a pair of vectors, t and u, where t contains the times at which the solution was computed and u contains the corresponding values of $u(t)$ .

clf
plot(t, u, '-o')
xlabel("t")
ylabel("u(t)")
title(("Solution of an IVP"));

You might want to know the solution at particular times other than the ones selected by the solver. That requires an interpolation. To do this automatically requires calling the solver with just one output argument, which is then supplied to deval to evaluate the solution at any time.

sol = ode45(f, [0, 4], u0);
u = @(t) deval(sol, t)';    % return a column vector
u(0:0.5:2)

Example 6.1.2

Let’s use solve_ivp from scipy.integrate to define and solve the initial-value problem

u'=\sin[(u+t)^2], \quad t \in [0,4], \quad u(0)=-1.

To create an initial-value problem for $u(t)$ , we must supply a function that computes $u'$ , an initial value for $u$ , and the endpoints of the interval for $t$ .

f = lambda t, u: sin((t + u) ** 2)
tspan = [0.0, 4.0]
u0 = array([-1.0])

Note above that even though this is a problem for a scalar function $u(t)$ , we had to set the initial condition as a one-component vector.

from scipy.integrate import solve_ivp
sol = solve_ivp(f, tspan, u0)

The resulting solution object has fields t and y that contain the values of the independent and dependent variables, respectively; those field names are the same regardless of what we use in our own codes.

print("t shape:", sol.t.shape)
print("u shape:", sol.y.shape)
plot(sol.t, sol.y[0, :], "-o")
xlabel("$t$"), ylabel("$u(t)$")
title(("Solution of $u' = sin((t+u)^2)$"));

t shape: (10,)
u shape: (1, 10)

You can see above that the solution was not computed at enough points to make a smooth graph. There is a way to request output at times of your choosing.

sol = solve_ivp(f, tspan, u0, t_eval=linspace(0, 4, 200))
plot(sol.t, sol.y[0, :], "-")
xlabel("$t$"), ylabel("$u(t)$")
title(("Solution of $u' = sin((t+u)^2)$"));

Another option is to enable interpolation to evaluate the solution anywhere after the fact:

sol = solve_ivp(f, tspan, u0, dense_output=True)
for t in linspace(0, 4, 6):
    print(f"u({t:.2f}) = {sol.sol(t)[0]:.4f}")

u(0.00) = -1.0000
u(0.80) = -0.8122
u(1.60) = -0.6204
u(2.40) = -0.4320
u(3.20) = -1.1139
u(4.00) = -1.8822

6.1.2Existence and uniqueness¶

There are simple IVPs that do not have solutions at all possible times.

Example 6.1.3 (Finite-time singularity)

Julia

MATLAB

Python

Example 6.1.3

The equation $u'=(u+t)^2$ gives us some trouble.

f(u, p, t) = (t + u)^2
ivp = ODEProblem(f, 1.0, (0.0, 1.0))
sol = solve(ivp, Tsit5());

┌ Warning: At t=0.7853839417697203, dt was forced below floating point epsilon 1.1102230246251565e-16, and step error estimate = 42.16290621054672. Aborting. There is either an error in your model specification or the true solution is unstable (or the true solution can not be represented in the precision of Float64).
└ @ SciMLBase ~/.julia/packages/SciMLBase/OKLBE/src/integrator_interface.jl:623

The warning message we received can mean that there is a bug in the formulation of the problem. But if everything has been done correctly, it suggests that the solution may not exist past the indicated time. This is a possibility in nonlinear ODEs.

plot(sol, label="";
    xlabel=L"t",  yaxis=(:log10, L"u(t)"),
    title="Finite-time blowup")

Example 6.1.3

The equation $u'=(u+t)^2$ gives us some trouble.

f = @(t, u) (t + u)^2;
u0 = 1;
tspan = [0, 1];
[t, u] = ode45(f, tspan, u0);

Warning: Failure at t=7.853789e-01.  Unable to meet integration tolerances without reducing the step size below the smallest value allowed (1.776357e-15) at time t.

The warning message we received can mean that there is a bug in the formulation of the problem. But if everything has been done correctly, it suggests that the solution simply may not exist past the indicated time. This is a possibility in nonlinear ODEs.

clf
semilogy(t, u)
xlabel("t")
ylabel("u(t)")
title(("Finite-time blowup"));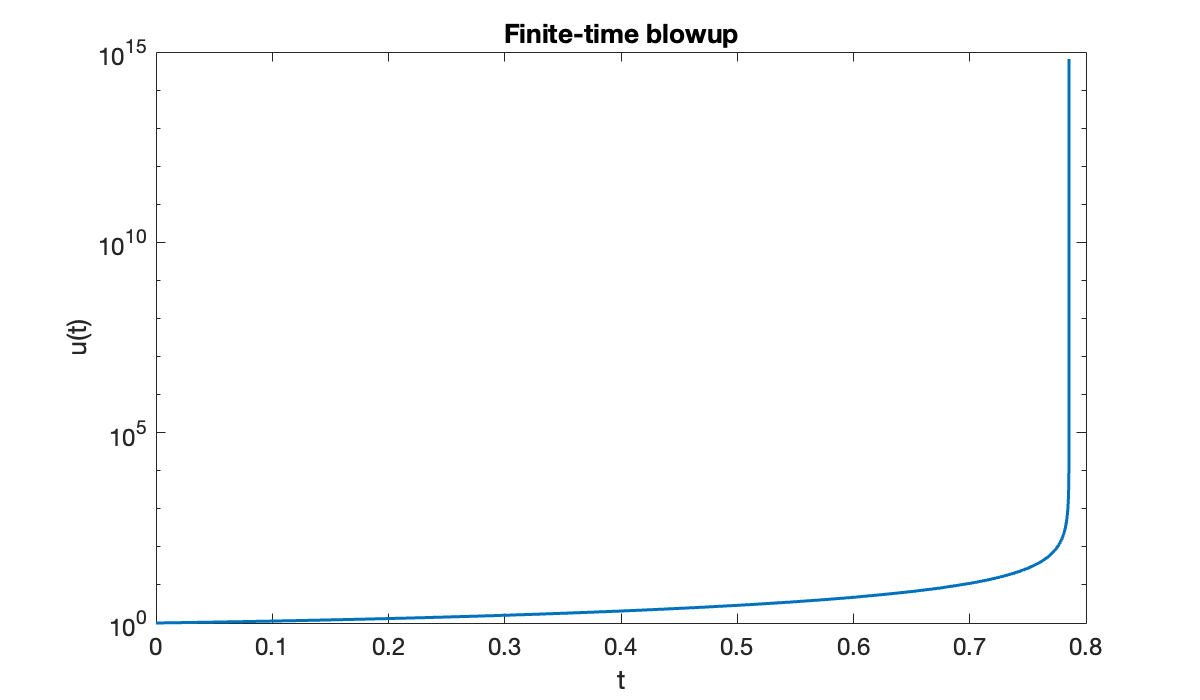

Example 6.1.3

The equation $u'=(u+t)^2$ gives us some trouble.

f = lambda t, u: (t + u) ** 2
sol = solve_ivp(f, [0.0, 1.0], [1.0])
if not sol.success:
    print(sol.message)

Required step size is less than spacing between numbers.

semilogy(sol.t, sol.y[0, :])
xlabel("$t$")
ylabel("$u(t)$")
title(("Blowup in finite time"));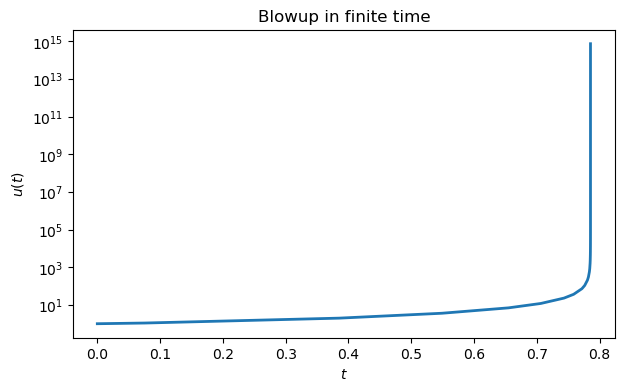

We can also produce an IVP that has more than one solution.

The following standard theorem gives us a condition that is easy to check and guarantees that a unique solution exists. But it is not the most general possible such condition, so there are problems with a unique solution that it cannot detect. We state the theorem without proof.

6.1.3Conditioning of first-order IVPs¶

In a numerical context we have to be concerned about the conditioning of the IVP. There are two key items in (6.1.1) that we might consider to be the data of the initial-value ODE problem: the function $f(t,u)$ , and the initial value $u_0$ . It’s easier to discuss perturbations to numbers than to functions, so we will focus on the effect of $u_0$ on the solution, using the following theorem that we give without proof. Happily, its conditions are identical to those in Theorem 6.1.1.

Numerical solutions of IVPs have errors, and those errors can be seen as perturbations to the solution. Theorem 6.1.2 gives an upper bound of $e^{L(b-a)}$ on the infinity norm (i.e., pointwise) absolute condition number of the solution with respect to perturbations at an initial time. However, the upper bound may be a terrible overestimate of the actual sensitivity for a particular problem.

Example 6.1.5 (Conditioning of an IVP)

Julia

MATLAB

Python

Example 6.1.5

Consider the ODEs $u'=u$ and $u'=-u$ . In each case we compute $\partial f/\partial u = \pm 1$ , so the condition number bound from Theorem 6.1.2 is $e^{b-a}$ in both problems. However, they behave quite differently. In the case of exponential growth, $u'=u$ , the bound is the actual condition number.

t = range(0, 3, length=800)
u = @. exp(t) * 1
lower, upper = @. exp(t) * 0.7, @. exp(t) * 1.3
plot(t, u;
    l=:black, ribbon=(lower, upper),
    leg=:none,  xlabel=L"t",  ylabel=L"u(t)",
    title="Exponential divergence of solutions")

But with $u'=-u$ , solutions actually get closer together with time.

u = @. exp(-t) * 1
lower, upper = @. exp(-t) * 0.7, @. exp(-t) * 1.3
plot(t, u;
    l=:black,  ribbon=(lower, upper),
    leg=:none,  xlabel=L"t",  ylabel=L"u(t)",
    title="Exponential convergence of solutions")

In this case the actual condition number is one, because the initial difference between solutions is the largest over all time. Hence the exponentially growing bound $e^{b-a}$ is a gross overestimate.

Example 6.1.5

Source

clf
for u0 = [0.7, 1, 1.3]    % initial values
    fplot(@(t) exp(t) * u0, [0, 3]), hold on
end
xlabel('t')
ylabel('u(t)')
title(('Exponential divergence of solutions'));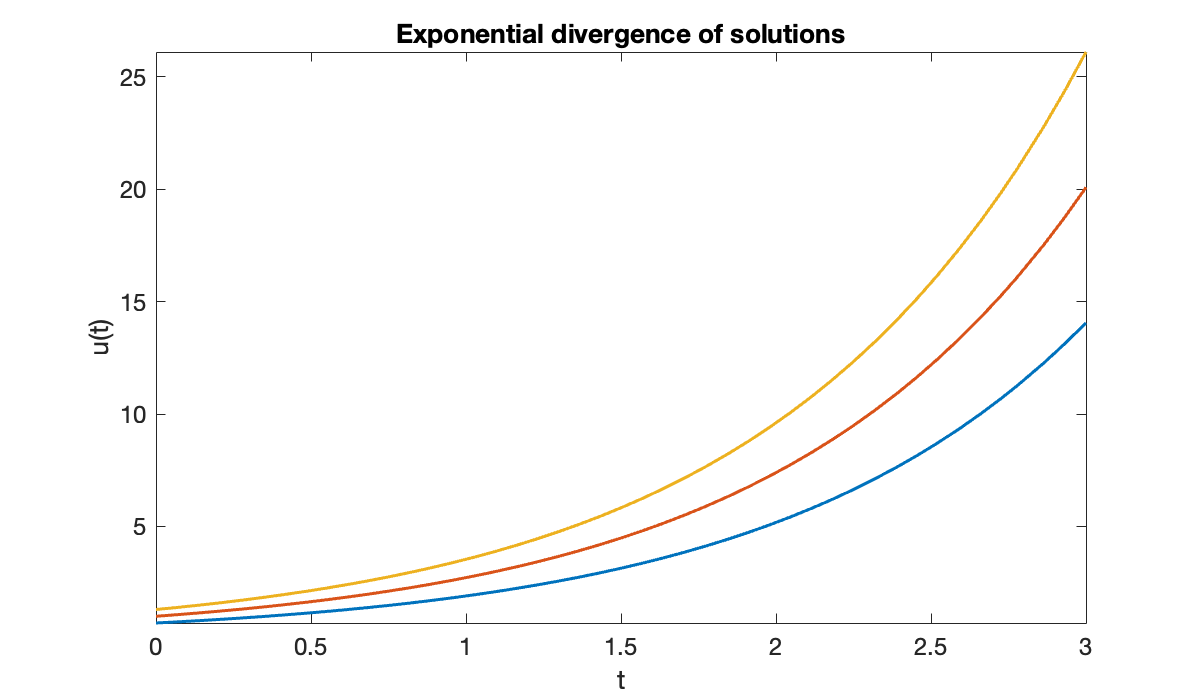

But with $u'=-u$ , solutions actually get closer together with time.

Source

clf
for u0 = [0.7, 1, 1.3]    % initial values
    fplot(@(t) exp(-t) * u0, [0, 3]), hold on
end
xlabel('t')
ylabel('u(t)')
title(('Exponential convergence of solutions'));

Example 6.1.5

t = linspace(0, 3, 200)
u = array([exp(t) * u0 for u0 in [0.7, 1, 1.3]])
plot(t, u.T)
xlabel("$t$")
ylabel("$u(t)$")
title(("Exponential divergence of solutions"));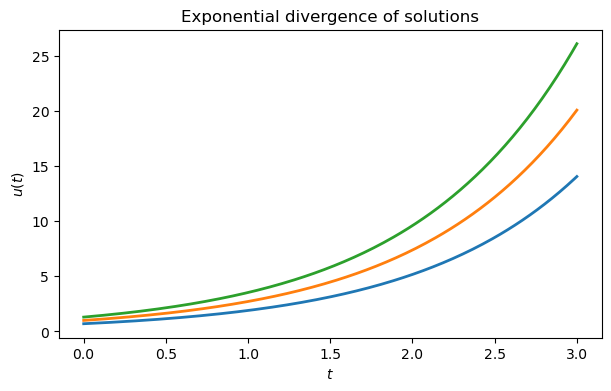

But with $u'=-u$ , solutions actually get closer together with time.

t = linspace(0, 3, 200)
u = array([exp(-t) * u0 for u0 in [0.7, 1, 1.3]])
plot(t, u.T)
xlabel("$t$")
ylabel("$u(t)$")
title(("Exponential convergence of solutions"));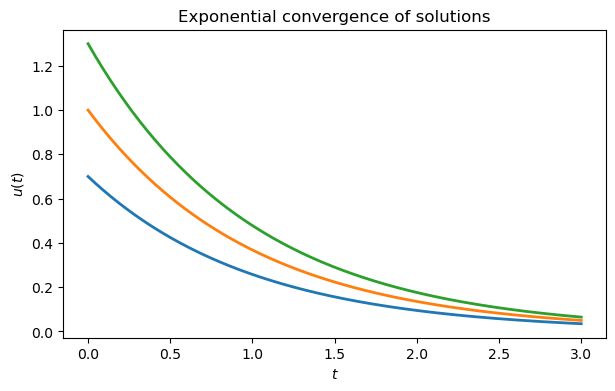

In this case the actual condition number is one, because the initial difference between solutions is the largest over all time. Hence, the exponentially growing upper bound $e^{b-a}$ is a gross overestimate.

In general, solutions can diverge from, converge to, or oscillate around the original trajectory in response to perturbations. We won’t fully consider these behaviors and their implications for numerical methods again until a later chapter.

6.1.4Exercises¶

Exercise 6.1.7

⌨ Experimental evidence (see Newton et al. (1981)) shows that a 300-mg oral dose of caffeine, such as might be found in a large mug of drip-brewed coffee, creates a concentration of about 8 $\mu{\rm g}$ /mL in blood plasma. This boost is followed by first-order kinetics with a half-life of about 6 hours (although this rate can vary a great deal from person to person). We can model the caffeine concentration due to one drink taken over half an hour via

x'(t) = -kx + C(t),\quad x(0)=0,

(6.1.8)

where $k=\log(2)/6$ and

C(t) = \begin{cases} 16, & 0\le t \le 0.5, \\ 0, & t > 0.5. \end{cases}

(6.1.9)

Use solve to make a plot of the caffeine concentration for 12 hours. Then change $k=\log(2)/8$ (half-life of 8 hours) and plot the solution again.

Exercise 6.1.8

⌨ A reasonable model of the velocity $v(t)$ of a skydiver is

\frac{dv}{dt} = -g + \frac{k}{m}v^2, \qquad v(0)=0,

(6.1.10)

where $g=9.8 \text{ m/sec}^2$ is gravitational acceleration, $m$ is the mass of the skydiver with parachute, and $k$ quantifies the effect of air resistance. At the US Air Force Academy, a training jump starts at about 1200 m and has $k=0.4875$ for $t<13$ and $k=29.16$ or $t\ge 13$ . (This is an oversimplification; see Meade & Struthers (1999).)

(a) Solve the IVP for $v$ for an 80-kg cadet for $t\in [0,200]$ , and plot the solution.

(b) The total distance fallen up to time $t$ is $\displaystyle\int_0^t v(s)\, ds$ . Use Function 5.7.1 to calculate and plot the altitude of the cadet as a function of time.

(c) In part (b), you should have found that the altitude becomes negative. Use Function 4.4.1 to determine accurately when the cadet reaches the ground.

References¶

Newton, R., Broughton, L. J., Lind, M. J., Morrison, P. J., Rogers, H. J., & Bradbrook, I. D. (1981). Plasma and Salivary Pharmacokinetics of Caffeine in Man. European Journal of Clinical Pharmacology, 21(1), 45–52. 10.1007/BF00609587
Meade, D. B., & Struthers, A. A. (1999). Differential Equations in the New Millennium: The Parachute Problem. International Journal of Engineering Education, 15(6), 417–424.

Preface

6. Initial-value problems for ODEs

Preface

Euler’s method